数学を得意にするためには、まず各公式に慣れることが必須です。
例えばlnxの微分や積分は頻出ですが、この公式、解き方について理解していますか。
ここでは、このlnxの微分や積分の計算方法、公式について解説していますので、参考にしてみてください
lnxの微分の公式、計算【自然対数:e】
それでは以下で底がe(ネイピア数)である自然対数lnの微分の公式、計算方法を確認していきます。
微分は積分よりも簡単であり、公式を覚えておけば容易に処理できます。
具体的には、(lnx)′ =1/x と公式そのままです。
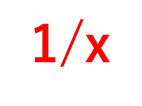
なお、後に解説のlnの積分(部分積分)の中でも、この微分を使用しますので、覚えておくといいです。
ポイントは
・logxという対数全般の微分結果は1/x
・自然対数(底がe)であっても同様に1/xが導関数の答え
ということを覚えておきましょう。
lnxの積分の公式、計算【自然対数】
lngxの積分では、部分積分の公式を用います。
具体的には、∫lnx dx =∫(x)’lnx dx
と、lnxの前にxを微分した「1」があるイメージをするといいです。
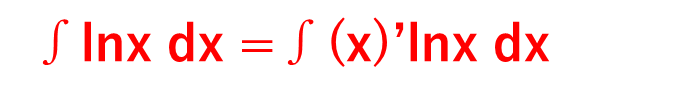
さらに、部分積分の公式を用いて変形していくと
=xlnx- ∫x (1/x) dx
=xlnx – ∫1 dx=xlnx – x +Cが答えとなります。
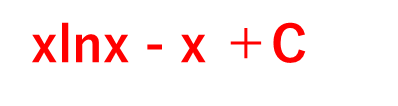
計算ミスしやすいため、丁寧に、式変形していくといいです。
これらがlnxの積分の公式、計算方法です。lnθ(シータ)でも記号のみ変えればOKです。
なお、底をeだけに限定しない一般的なlogxの微分・積分結果はこちらで解説していますので、参考にしみてくださいね。

まとめ lnxの積分や微分の公式、計算【自然対数】
このでは、lnxの積分、微分の公式、計算方法について確認しました。logθ(コサイン)であっても処理方法は同じです。
logxの微分、積分はよく出てくるため、この機会に覚えておくといいです。
さまざまな計算に慣れ、数学をより楽しんでいきましょう。