この記事では「エクセルでの二項分布のグラフの作り方・計算方法」について、解説していきます。
二項分布とは
「”勝ち” ”負け”のような結果が2つの試行をN回行った際に勝ち数がM回となる確率」
の分布を意味しますが、エクセルでどのようにデータを用意し、かつグラフ化するかは相応の知識が必要となります。
今回はエクセルで二項分布を扱うにおいて、下記2点の観点から説明します。
・計算方法(どのような関数を使用するか)
・グラフ化(適したグラフ種とは?)
それでは、各場面において順番に説明していきます。
エクセルでの二項分布の計算方法【関数など】
エクセルにて二項分布の計算方法について「打率.315の打者が20打席バッティングしたときのヒット数」を例に説明します。
確率を出力するセルに
「=BINOM.DIST(A2,$G$1, $E$1, SWITCH($I$1, “累計分布関数”, TRUE, “確率質量関数”, FALSE))」
と入力します。
条件設定については、打率=.315、打席数=20とします。

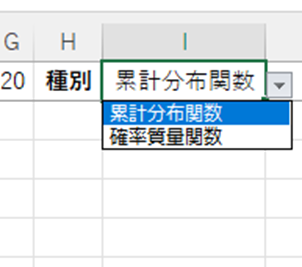
種別については、入力規則を用いて「累計分布関数」「確率質量関数」のどちらかを選択させるようにします。
リボンより「データ」→「データの入力規則」→「データの入力規則」をクリックします。
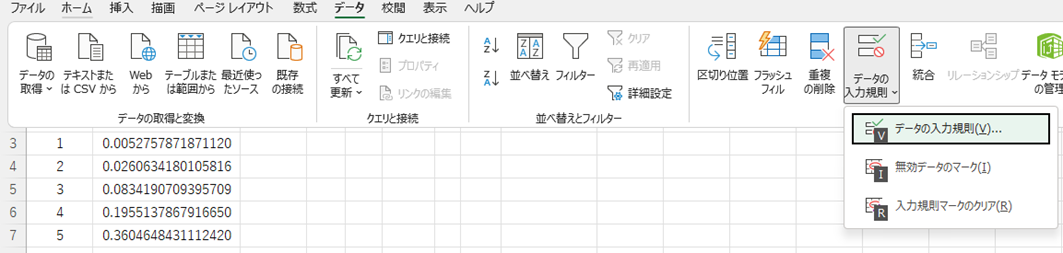
「データの入力規則」ダイアログで「設定」タブを選択し、入力値の種類でリストを選択し、元の値に
「累計分布関数, 確率質量関数」と入力します。
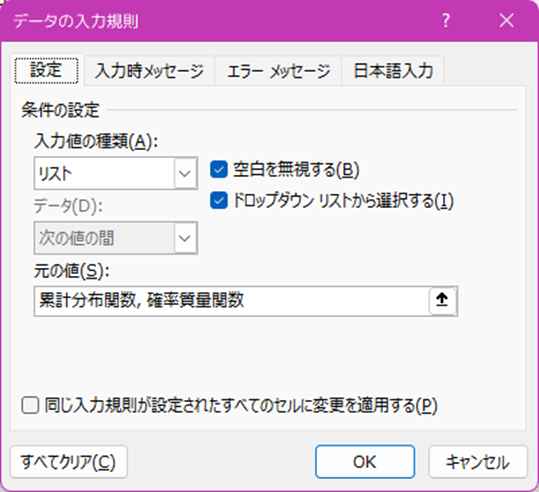
OKボタンを押し、ドロップダウンに2つが含まれていれば問題なしです。
数式について詳細を解説します。
使用する各関数について
=BINOM.DIST (成功数, 試行回数, 成功率 関数形式)
=SWITCH (式, 値1, 結果1,[値2, 結果2], …)
と入力します。
試行回数=打席数、成功率=打率に設定します。
また、関数形式については「TRUE or FALSE」を設定しますが、より機能性を求めるため、SWITCH関数を用いて、設定変更できるようにします。
SWITCH関数は式の値が「=値1なら結果1、=値2なら結果2」を出力するものです。
ここまで入力できたらENTERキーを押して、計算結果が表示されるかを確認します。

全ての行に式をコピーして完成させましょう。
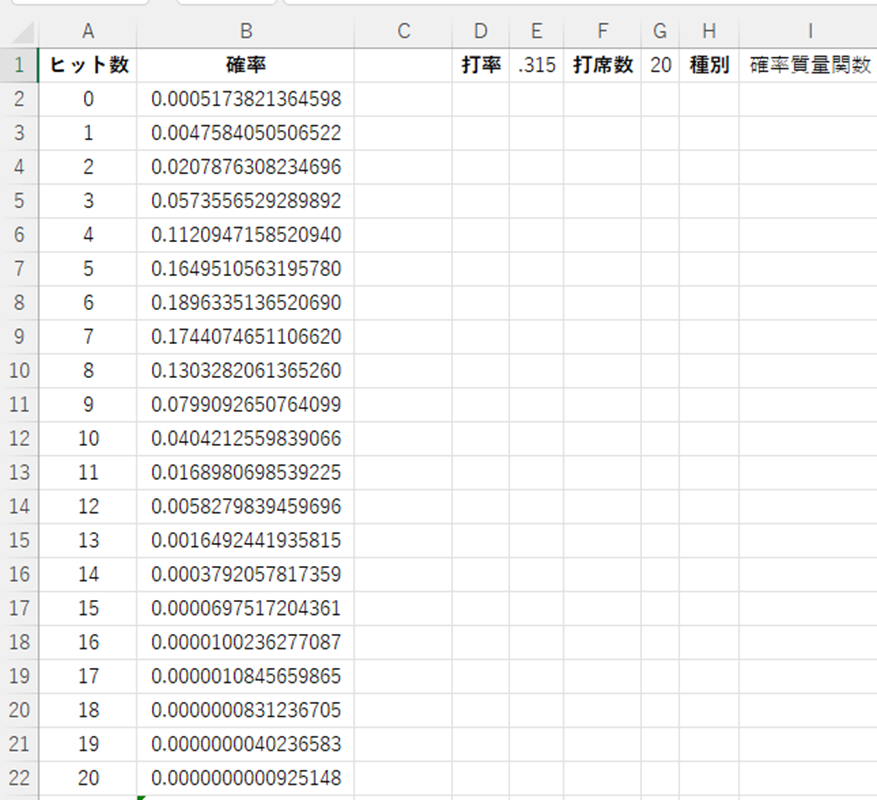
いくつか注意事項を説明します。
試行回数及び成功率=打率については「$○$△(絶対参照)」にしましょう。
間違えると想定している計算がされません。

また、打席数は20で設定されているので、それ以上のヒット数を計算しようとすると、エラーとなります。
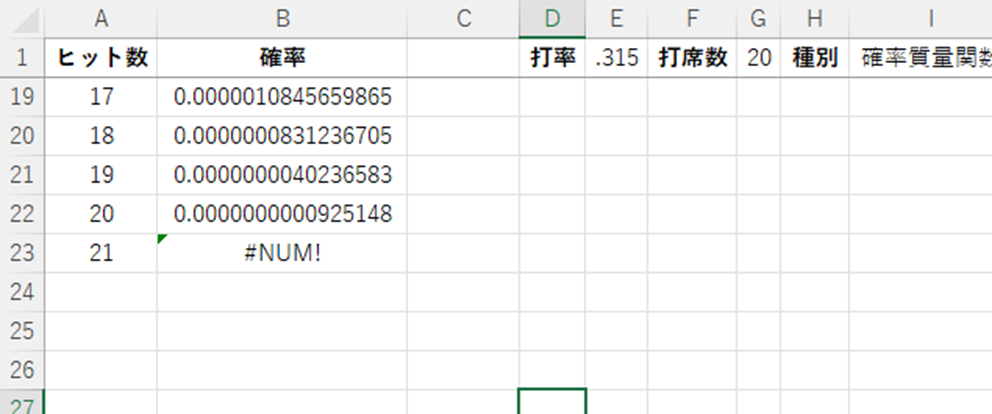
エクセルでの二項分布のグラフの作り方【書き方】
前項で作成したデータを用いてエクセルでの二項分布のグラフを作成します。
データを選択した状態で、リボン「挿入」を開き、下記の赤枠をクリックします。
「グラフの挿入」ウィザードでグラフ種を選択します。
適用できるグラフ種は「散布図・折れ線・集合縦棒」などがありますが、要求に応じて使い分けることになるでしょう。
本例では「折れ線」を採用しています。

OKボタンを押すと、グラフが描画されます。

ここで、種別を「累計分布関数」に切り替えるとグラフが切り替わります。
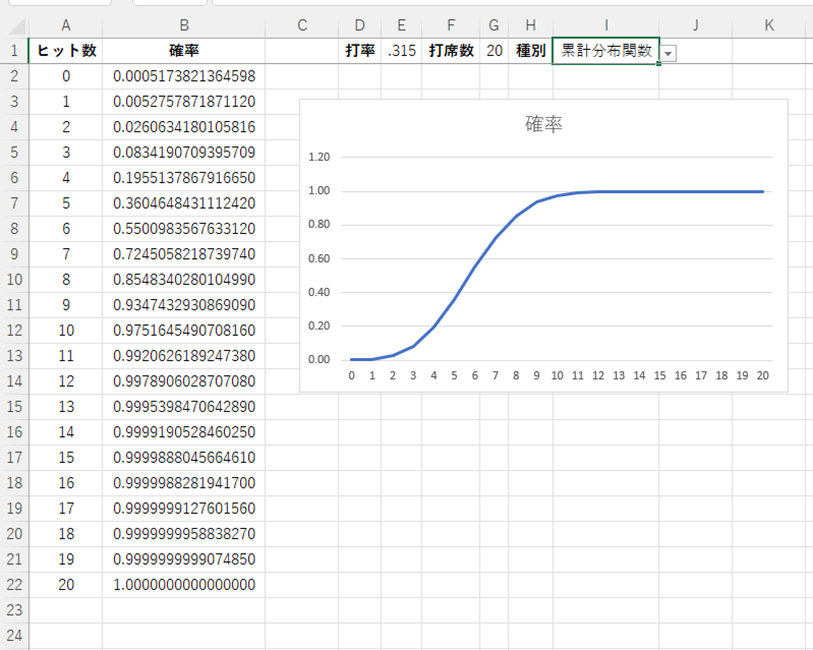
まとめ エクセルでの二項分布のグラフの作り方・計算方法
この記事では「エクセルでの二項分布のグラフの作り方・計算方法」について解説しました。
一見難しそうでもありますが、エクセルには二項分布をはじめとする統計処理するための関数がたくさん用意されています。
使い方を勉強して、実践で活用できるようにしましょう。