数学を得意にするためには、まず各公式に慣れることが必須です。
例えばlog3xやlog4xなど「logaxの微分」は頻出ですが、この公式、解き方について理解していますか。
ここでは、このlog3xやlog4xなど「logaxの微分」の計算方法、公式について解説していますので、参考にしてみてください
log3xの微分の公式・計算方法【logax:ログ】
それでは以下で、logaxの代表といえるlog3xの微分の公式、計算方法を確認していきます。なお記号にθを用いたlog3θ(ログ)の微分方法も全く同じです。
微分は積分よりも簡単であり、公式を覚えておけば容易に処理できます。
具体的には、(log3x)′ =1/3x (3x)′=3/3x =1/x
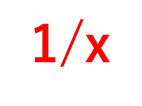
ポイントは
・logxの微分は1/xとなること
・中身を微分したもの(3x)′もかけること
です。
なお、一般式のlogaxの微分はaの値がどのような正の整数でも「1/x」となると覚えておきましょう(途中の式で、(ax)’ /ax = a/ax =1/xと変換されるため)。
計算ミスしやすいため、丁寧に、式変形していくといいです。
これらがlog3xの微分の公式、計算方法です。log2θ(シータ)でも記号のみ変えればOKです。
なお、log2xの微分・積分の計算方法・公式はこちらで解説しているため、併せて確認してみてくださいね。
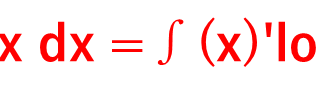
log4xの微分の公式・計算方法【logax:ログ】
続いても、logaxの代表といえるlog4xの微分の公式、計算方法を確認していきます。なお記号にθを用いたlog4θ(ログ)の微分方法も全く同じです。
微分は積分よりも簡単であり、公式を覚えておけば容易に処理できます。
具体的には、(log4x)′ =1/4x (4x)′=4/4x =1/x
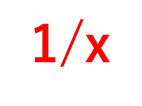
ポイントは
・logxの微分は1/xとなること
・中身を微分したもの(4x)′もかけること
です。
改めて記載しますが、一般式のlogaxの微分はaの値がどのような正の整数でも「1/x」となると理解しておくといいです(途中の式で、(ax)’ /ax = a/ax =1/xと変換されるため)。
まとめ log2xやlog3xの微分の公式や計算方法【ログ:log2θやlog3θ】
ここでは、og3xやlog4xなど「logaxの微分」の計算方法、公式について確認しました。logaθ(ログ)であっても処理方法は同じです。
logaxの微分はよく出てくるため、この機会に覚えておくといいです。
さまざまな計算に慣れ、数学をより楽しんでいきましょう。