数学を得意にするためには、まず各公式に慣れることが必須です。
例えば1/sinx(1/sinθ)の微分や積分は頻出ですが、この公式、解き方について理解していますか。
ここでは、この1/sinx(1/sinθ)の微分や積分の計算方法、公式について解説していますので、参考にしてみてください。
1/sinxの積分の公式、計算【1/sinθ(コサイン)】
それでは以下で、1/sinxの積分の公式、計算方法を確認していきます。なお記号にθを用いた1/sinθ(コサイン)の積分方法も全く同じです。
まずは、∫1/sinx dxの分子と分母に、sinxをかけましょう。すると∫sinx/sin^2 x dx と変形できます。
ここで、sin^2 x=1-cos^2 xを代入すると、 =∫sinx/(1-cos^2 x)dx ・・①となります。
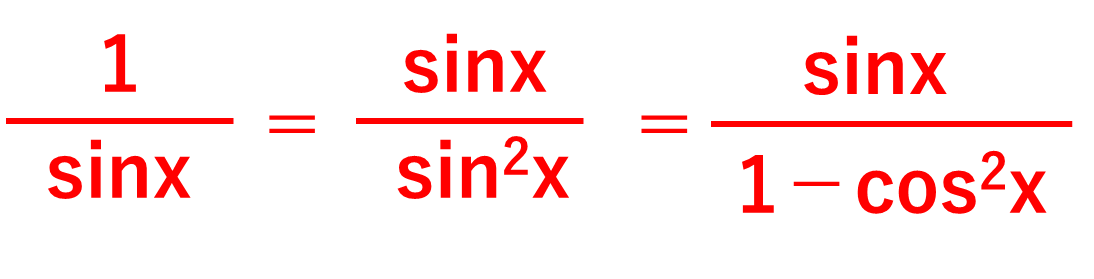
さらに、cosx=tとし、両辺を微分して整理すると、dt/dx=-sinxと処理できるのがわかるでしょう。
つまり、dx= -dt/ sinx となるのです。
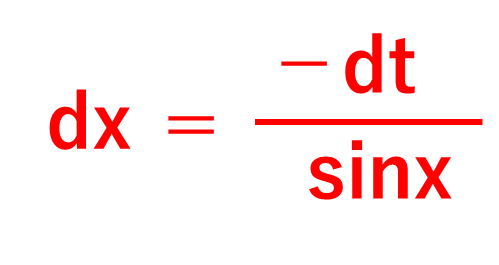
①式に戻ると、sinxが上手く消え、=∫1/(t^2-1)dt と式変形できます。
ここで「-dt」と、マイナスがつくため、1-cos^2 xの順序が入れ替わっています。
さらに、∫1/(t^2-1)dtの形では1/(t-1)-1/(t+1)といった形に分けるといいため
∫1/(t^2-1)dt = 1/2∫{1/(t-1)-1/(t+1)}dt =1/2 log{(t-1)/(t+1)}+C(積分定数)
と処理できるわけです。
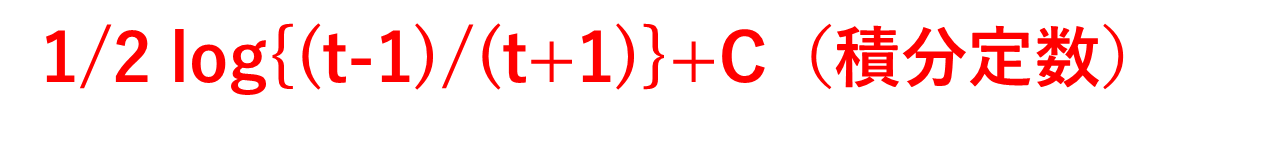
最後に元のt=cosx を入れ直せば、答えが 1/2 log{(cosx-1)/(cosx+1)} +Cとなります。
なお、積分区間も記載されている場合では、その対応も変化するため注意するといいです。「最初の分子、分母にsinをかけるのがポイント」のため、これを理解しておきましょう。
これらが1/sinxの積分の公式、計算方法です。1/sinθ(シータ)でも記号のみ変えればOKです。
1/sinxの微分の公式・計算方法【1/sinθ(コサイン)】
今度は1/sinxの微分の公式、計算方法を確認していきます。なお記号にθを用いた1/sinθ(コサイン)の積分方法も全く同じです。
微分は積分よりも簡単であり、公式を覚えておけば容易に処理できます。
具体的には、 (1/sinx)′ =(sinx ^-1)′ =(-1)sinx^(-1-1)(sinx)′=-cosx/sin^2 xとなります。

ポイントは
・1/sinx=sinx ^-1
・微分では、肩の係数が前に来て、元の係数が-1されること
・中身を微分したもの(sinx)′もかけること
ですね。
まとめ 1/sinxの微分、積分の公式、計算【1/sinθ(サインx分の1)】
このでは、1/sinxの積分、微分の公式、計算方法について確認しました。1/sinθ(シータ)であっても処理方法は同じです。
1/sinxの微分、積分はよく出てくるため、この機会に覚えておくといいです。
さまざまな計算に慣れ、数学をより楽しんでいきましょう。