この記事では「エクセルでの偏差値の求め方や分布のグラフの作成方法」について、解説していきます。
偏差値という言葉自体は馴染みがあるものの「偏差値ってどういう計算で出された値ですか?」と質問したら、しっかりと答えらない人がほとんどではないでしょうか。
このような背景も踏まえ、今回は下記に焦点を当つつ処理方法を見ていきま。
・そもそも偏差値って何?
・エクセルで偏差値を求めるには?
・偏差値の分布をグラフにするには?
それでは、順番に説明していきます。
エクセルでの偏差値の求め方【計算方法】
エクセルにて偏差値を計算していく前に、その定義を確認していきます。
現在、大学受験で採用されている偏差値の定義はこちらです。
この中で
・平均点→AVERAGE
・標準偏差→STDEV.P ただしOffice 2007以降に限る
を用いれば、シンプルな計算式で偏差値がわかります。
下記サンプルデータで解説します。
C列に偏差値を求める列を作成し、この列の2行目(C2セル)に「=(B2-AVERAGE($B$2:$B$29))/STDEV.P($B$2:$B$29) *10+50」と入力します。
数式について解説します。
関数についてはそれぞれ、
= AVERAGE (数値1, [数値2], …)
= STDEV.P (数値1, [数値2], …)
と入力します。
平均点と標準偏差を求め、偏差値の定義に当てはめていきます。
ENTERキーを押すと、偏差値が計算されます。
すべての行に計算式をコピー(C2セルの右下にカーソルを合わせると出てくる十字をドラッグ&ドロップ)して、全受験者の偏差値を計算しましょう。
これで、エクセルでの偏差値を一気に計算できます。
エクセルでの偏差値のグラフ(分布など)の作成方法
先ほどのサンプルデータの偏差値の分布をグラフで描いてみましょう。
40未満: ○人
41~49: ○人
51~59: ○人
60以上: ○人
といったよう階級値ごと(偏差値事)のヒストグラムをすべく、下記のようにもう1つ別の表を作りましょう。
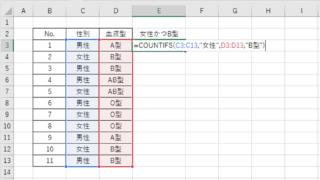
具体的には階級値を以下のよう入力した上で、=COUNIFS(偏差値の範囲の絶対参照,各階級値(以下では”<=”かE2セル))と入れましょう。
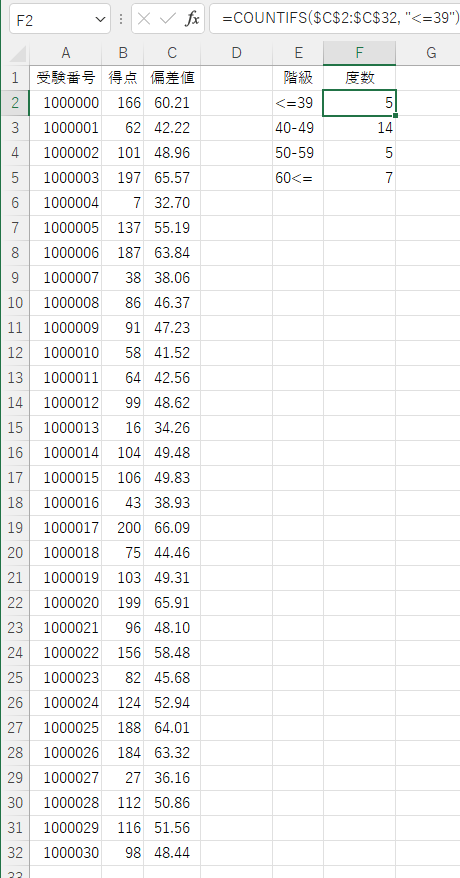
度数で使用している数式について説明します。
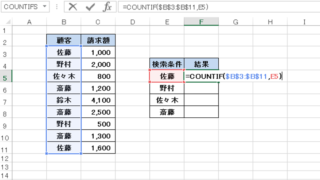
COUNTIFS関数は次のように入力します。
=COUNTIFS(検索条件範囲1, 検索条件1, [検索条件範囲2, 検索条件2], …)
計算される値は下記のとおりです。
COUNTIFS(**, “<=X1”): X1以下のデータ数
COUNTIFS(**, “>=X2”, **, “<=X3”): X2以上X3以下のデータ数
COUNTIFS(**, “>=X4”): X4以上のデータ数
各数式の先頭に「=」を付け、ENTERキーを押すと、各値が出力されます。
なお、
・COUNTIFS関数にて複数条件(andやor)で処理する方法の詳細はこちら
で解説していますので、併せてチェックしてみてくださいね♪
偏差値のグラフ作成に戻ります。
作成した度数分布表を選択し、「グラフ」ダイアログを開き、「集合縦棒」を選択します。
OKボタンを押すと、グラフが描画されます。
なお、グラフを右クリックし、「データ系列の書式設定」を開き、要素の間隔を0%にすることで、よりヒストグラムに近い見た目に調整できます。
棒グラフの体裁を整える際には、こちらの棒グラフ関係の処理のまとめ
を参考にしてみてくださいね。

おすすめしないがグラフの挿入→ヒストグラムでも処理可能
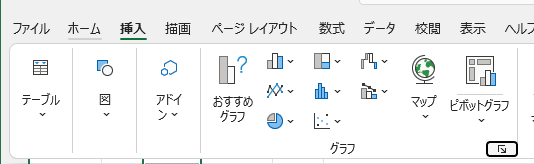
リボン「挿入」を開き、その中の「グラフ」グループの右下の矢印をクリックします。
「グラフの挿入」ダイアログで「すべてのグラフ」タブを開き、「ヒストグラム」を選択します。
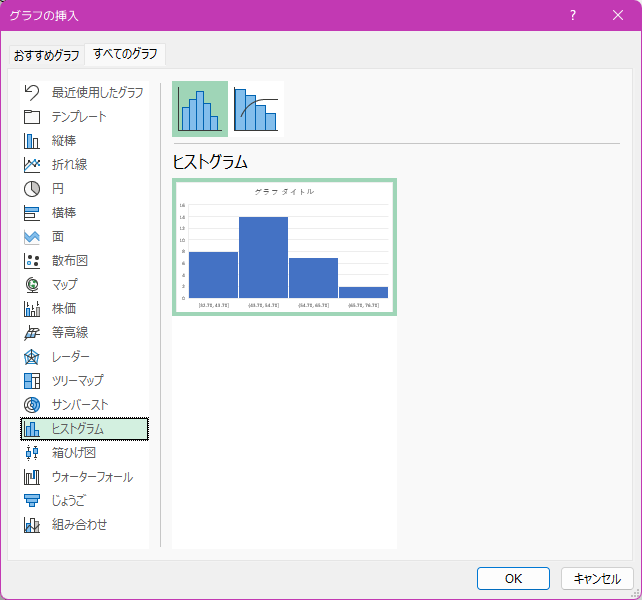
OKボタンを押すと、偏差値のヒストグラムが表示されます。
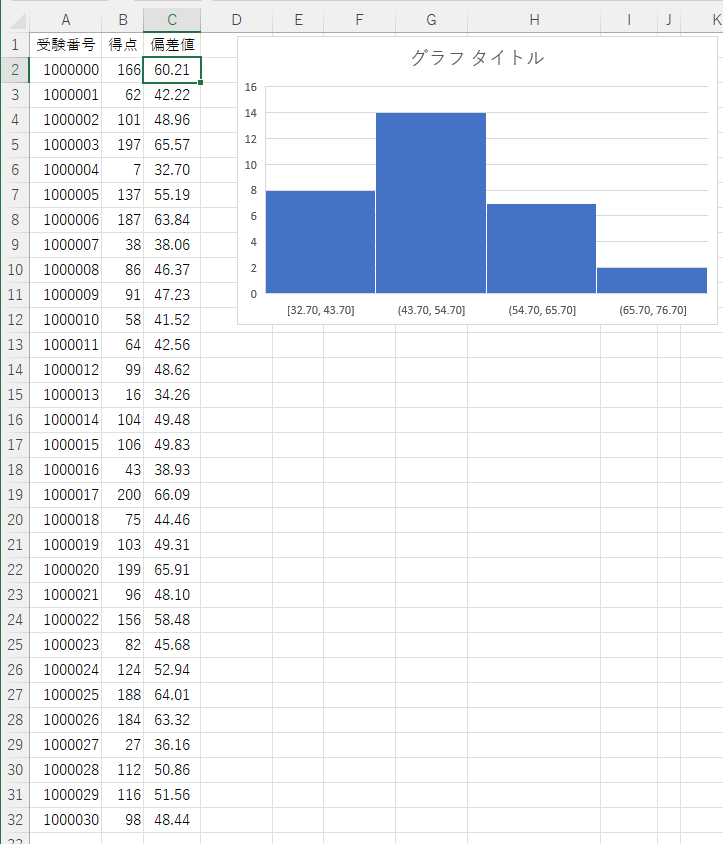
しかし、この手法では意味の分かりにくいグラフが描画されてるため、少々手間ですが自身で階級値ごとの偏差値の度数を求める方がおすすめです。
まとめ エクセルでの偏差値の求め方や分布のグラフの作成方法
この記事では「エクセルでの偏差値の求め方や分布のグラフの作成方法」について解説しました。
学校内で行った試験における偏差値を計算したい、場合にご活用ください。
各生徒の実力の見える化を行い、より効率的な学習方法を確立することで生徒と学校双方が最大の利益を得られることが望ましいといえます。