数学を得意にするためには、まず各公式に慣れることが必須です。
例えば1/tanx(1/tanθ)の微分や積分は頻出ですが、この公式、解き方について理解していますか。
ここでは、この1/tanx(1/tanθ)の微分や積分の計算方法、公式について解説していますので、参考にしてみてください。
1/tanxの積分の公式、計算【1/tanθ(タンジェント分の1)】
それでは以下で、1/tanxの積分の公式、計算方法を確認していきます。なお記号にθを用いた1/tanθ(タンジェント分の1)の積分方法も全く同じです。
まずは、1/tanxにおいて、tanx=sinx/cosx を代入しましょう。
つまり ∫1/tanx dx =∫cosx/sinx dxとなるわけです。
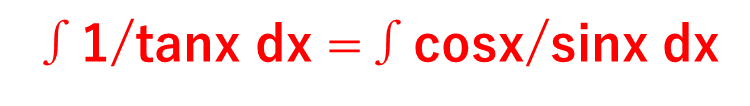
ここで、cosxがsinの微分であり、かつsinxが分母に来ていることから
=∫(sinx)’/sinx dx =log(sinx)+C(積分定数)
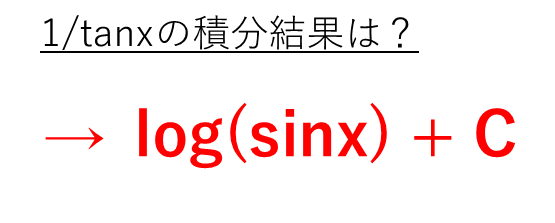
と処理できるのがわかりますね。
なお、積分区間も記載されている場合では、その対応も変化するため注意しましょう。
これらが1/tanxの積分の公式、計算方法です。1/tanθ(シータ)でも記号のみ変えればOKです。
1/tanxの微分の公式、計算【1/tanθ(タンジェント)】
今度は1/tanxの微分の公式、計算方法を確認していきます。なお記号にθを用いた1/tanθ(シータ)の積分方法も全く同じです。
通常は微分は積分よりも処理は簡単ですが、今回の1/tanxでは逆に複雑となるため、気をつけましょう。
具体的には、(1/tanx)′ =(tanx ^-1)′ =(-1)tanx^(-1-1)(tanx)′= -(1/cos^2x)/tan^2x・・・①と変形できます。
この時(tanx)′= 1/cos^2x の公式を活用しています。
①式にtanx=sinx / cosx も代入しますと、-(1/cos^2x)/(sin^2x/cos^2x)==-1/sin^2xと導出できるわけです。
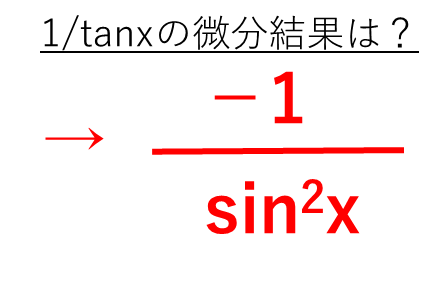
ポイントは
・1/tanx=tanx ^-1と書けること
・微分では、肩の係数が前に来て、元の係数が-1されること
・中身を微分したもの(tanx)′も掛けること
・(tanx)′= 1/cos^2x
あたりですね。
同じ三角関数を分母に含む積分でも1/sinxや1/cosxの積分の方が難しいため、併せて理解しておくといいです。


まとめ 1/tanxの微分、積分の公式、計算【1/tanθ(タンジェントx分の1)】
このでは、1/tanxの積分、微分の公式、計算方法について確認しました。1/tanθ(シータ)であっても処理方法は同じです。
1/tanxの微分、積分はよく出てくるため、この機会に覚えておくといいです。
さまざまな計算に慣れ、数学をより楽しんでいきましょう。

















