科学的な解析を行う際には、関係する専門用語の意味を理解していないと対処できないことが多いです。
例えば、電気的な分野においてよく導電率や抵抗率などの用語を耳にすることがありますが、これらはどのような意味を持つのか理解していますか。
ここでは、これら導電率(電気伝導率)や抵抗率(比抵抗)の意味や違い、各々の換算(変換)方法について確認していきます。
抵抗率(比抵抗)と導電率(電気伝導率)の違いと換算(変換)方法【意味は?】
それでは、電気的な用語である抵抗率と導電率の意味や違いについて確認していきます。
まず、抵抗率の意味について考えるために、以下のような電気抵抗があるとします。
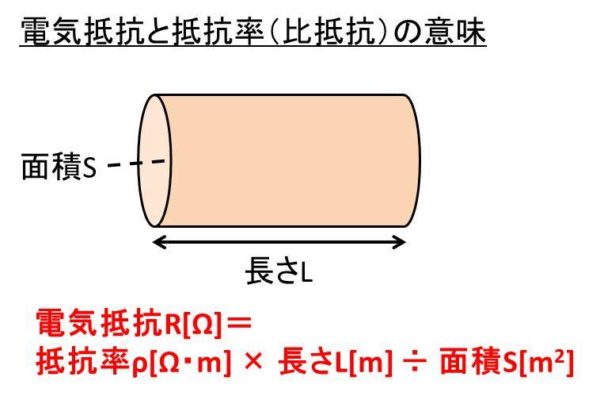
このとき、電気抵抗R[Ω]=抵抗率ρ[Ω・m] × 長さL[m] ÷ 面積S[m2] で表すことができ、抵抗率は物質固有の電気の流れにくさを表す指標といえます。
抵抗率基準の式にしますと、抵抗率(比抵抗)ρ[Ω・m] =電気抵抗R[Ω]÷ 長さL[m]×面積S[m2]で計算することが可能なのです。
つまり、同じ長さ、同じ断面積の材料であればその抵抗率の数値が大きいほど、電気抵抗が大きくなるので電気が流れにくいということを示しているわけです。
一方で、導電率の意味としては、逆に電気の流れやすさを意味しており、抵抗率の逆数をとったものが導電率となるのです。

なお、導電率の単位としては1/(Ω・m)ですが1/Ω=S(ジーメンス)という単位を活用し、S/m(ジーメンスパーメートル)という単位を使用するのが基本です。
導電率(電気伝導率)と抵抗率(比抵抗)の換算(変換)の計算問題【求め方】
それでは、導電率と抵抗率の換算に慣れるためにも以下の問題を解いていきましょう。
例題1
ある材質の抵抗率は9×10^-8Ω・mです。この材質の導電率はいくらと換算できるのでしょうか。
解答1
導電率=1 ÷ (9 × 10^-8)= 約1.1×10^7S/mと変換できました。
逆に、導電率(電気伝導率)から抵抗率への換算も行ってみましょう。
例題2
ある材質の導電率(電気伝導率)は2 × 10^7 S/mです。この材料の比抵抗(抵抗率)はいくらと求められるでしょうか。
解答2
こちらでも上の導電率と比抵抗の換算式を元に計算していきます。
逆数をとればいいため、1 ÷ (2×10^7)=5× 10^-8 Ω・mと変換することができました。
両方とも良く使用する用語であるため、しっかりと覚えておくといいです。
まとめ 電気伝導率と比抵抗(低効率)との換算(変換)方法
ここでは、抵抗率(比抵抗)と導電率(電気伝導率)の変換方法について確認しました。
比抵抗とは、物質固有の電気の流れにくさを表す指標といえ、抵抗率=電気抵抗÷長さ×面積で求めることができます。
一方で、導電率は電気の流れやすさを示すものであるため、導電率=1/抵抗率という逆数の関係が成立するのです。
導電率の単位は基本的にはS/mであり、抵抗率はΩ・mであることも併せて押さえておくといです。
導電率と抵抗率の違い等、科学用語を理解し、業務に活かしていきましょう。