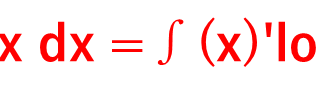数学を得意にするためには、まず各公式に慣れることが必須です。
例えばcos3x(cos3θ)の微分や積分は頻出ですが、この公式、解き方について理解していますか。
ここでは、このcos3x(cos3θ)の微分や積分の計算方法、公式について解説していますので、参考にしてみてください。
cos3xの積分の公式、計算【cos3θ(コサイン)】
それでは以下で、cos3xの積分の公式、計算方法を確認していきます。なお記号にθを用いたcos3θ(コサイン)の積分方法も全く同じです。
まずは、cos3xにおける3x=tとしましょう。この置換がcos3xの積分の最初のポイントですね。
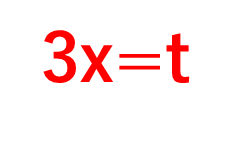
ここで上の3x=tをtについて微分しましょう。
すると、3dx/dt=1⇄ dx/dt=1/3⇄dx=dt/3と変換できるわけです。
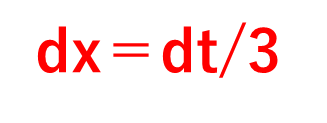
この状態で、コサイン3xの積分の本題に入っていきます。
∫cos3x dx=1/3 ∫cost dt = 1/3 ∫cost dt
と整理できるのがわかるでしょう。
この時、積分区間も記載されている場合では、その対応も変化するため注意するといいです。
これをとくと、1/3 sint +C(cは定数)となります。
さらに最初に3x=tとしたため、元に戻すと、1/3 sin3x +C が答えとなります。

これらがcos3xの積分の公式、計算方法です。cos3θ(コサイン)でも記号のみ変えればOKです。
cos3xの微分の公式、計算【cos3θ(コサイン)】
今度はcos3xの微分の公式、計算方法を確認していきます。なお記号にθを用いたcos3θ(コサイン)の積分方法も全く同じです。
微分は積分よりも簡単であり、公式を覚えておけば容易に処理できます。
具体的には、 (cos3x)′ =−sin3x (3x)′=−3sin3xとなります。
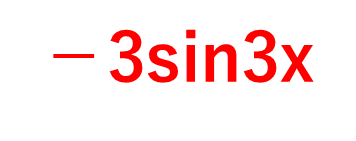
ポイントは
・cosxの微分はーsinxとなること
・中身を微分したもの(3x)′もかけること
ですね。
まとめ cos3xの微分、積分の公式、計算【cos3θ(コサイン)】
このでは、cos3xの積分、微分の公式、計算方法について確認しました。cos3θ(コサイン)であっても処理方法は同じです。
cos3xの微分、積分はよく出てくるため、この機会に覚えておくといいです。
さまざまな計算に慣れ、数学をより楽しんでいきましょう。